▶ Les angles

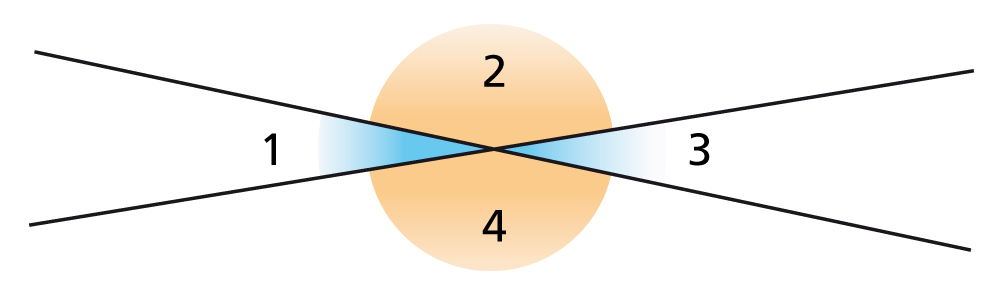
Deux droites sécantes forment quatre angles : deux paires d’angles égaux et opposés par le sommet.
▶ Dans une figure géométrique, un angle correspond à une ouverture entre deux segments ou deux demi-droites de même origine. Un angle a deux côtés et un sommet. Les sommets des polygones sont des angles.
▶ Un angle se mesure en degrés, à l’aide d’un rapporteur. Un angle qui mesure 90° est dit « droit ».Selon leur ouverture, on distingue : l’angle aigu (inférieur à l’angle droit), l’angle droit, l’angle obtus (supérieur à l’angle droit mais inférieur à l’angle plat), l’angle plat (c’est le double d’un angle droit et ses deux côtés sont alignés) ; il mesure 180°.
▶ La bissectrice d’un angle est une demi-droite issue de son sommet, qui le partage en deux parties égales : c’est l’axe de symétrie de l’angle.

▶ Les triangles

Trois droites qui se coupent en trois points différents forment un triangle. On le dessine avec la règle et le compas, si l’on connaît les mesures de ses trois côtés, ou avec la règle et le rapporteur, si l’on connaît les mesures d’un angle et de deux côtés ou d’un côté et de deux angles.
Les triangles particuliers :
▶ Le triangle rectangle, qui a un angle droit.
▶ Le triangle isocèle, qui a deux côtés (et deux angles) de même mesure.
▶ Le triangle isocèle rectangle, qui a deux côtés (et deux angles) de même mesure et le troisième angle, droit.
▶ Le triangle équilatéral, qui a trois côtés et trois angles de même mesure. Chaque angle mesure 60°.Quand un triangle ne correspond à aucun de ces triangles particuliers (aucun angle droit et ses côtés et ses angles sont de mesures différentes), on dit qu’il est « quelconque ».